最近被十一黄金周报复性旅游的新闻刷屏，难以想象许多景点空旷无人的景象仅仅发生在半年多前。当时国内虽然实时汇总发布新冠日增数据，但很多人对数据的真实性依然存疑，我有不少同事都说不能全盘接受中国的数据，得对数据有个house view（内部评估）。

我当时也没细究，因为觉得评估数据真假不是靠我一己之力就能完成的，遂作罢。最近突然读到 Benford’s law(本福特定律), 不禁懊悔地拍大腿，我早就该用这个定律检验数据呀！亡羊补牢，未为晚也，那就开始检验吧！

首先要介绍下 Benford’s law。这其实是个从日常生活中总结出来的定律，初次听说觉得不太符合直觉，但愈用愈香。维基词条是这么解释的：数字首位（1，2，3……9，不包括0）出现的概率并不相同（1/9），而是呈“头重脚轻”式分布，简单来说，1打头的概率大概是30%，远远高于9打头的概率（5%）。

这个定律主要适用于产生过程相对随机的数据，比如说银行账单、人口增长、门牌号、死亡率、物理常数、新闻报道中出现的数字等等…… 就拿身边触手可及的例子来说吧。我打开微信钱包，截下了最近3页的流水。稍加统计后就发现，1打头的概率居然高达24%，远高于11%，与定律预测的30%也八九不离十。如果我继续往下翻调出更多数据，或者用我自己更加常用的银行账单做例证，比例就更接近30%啦。

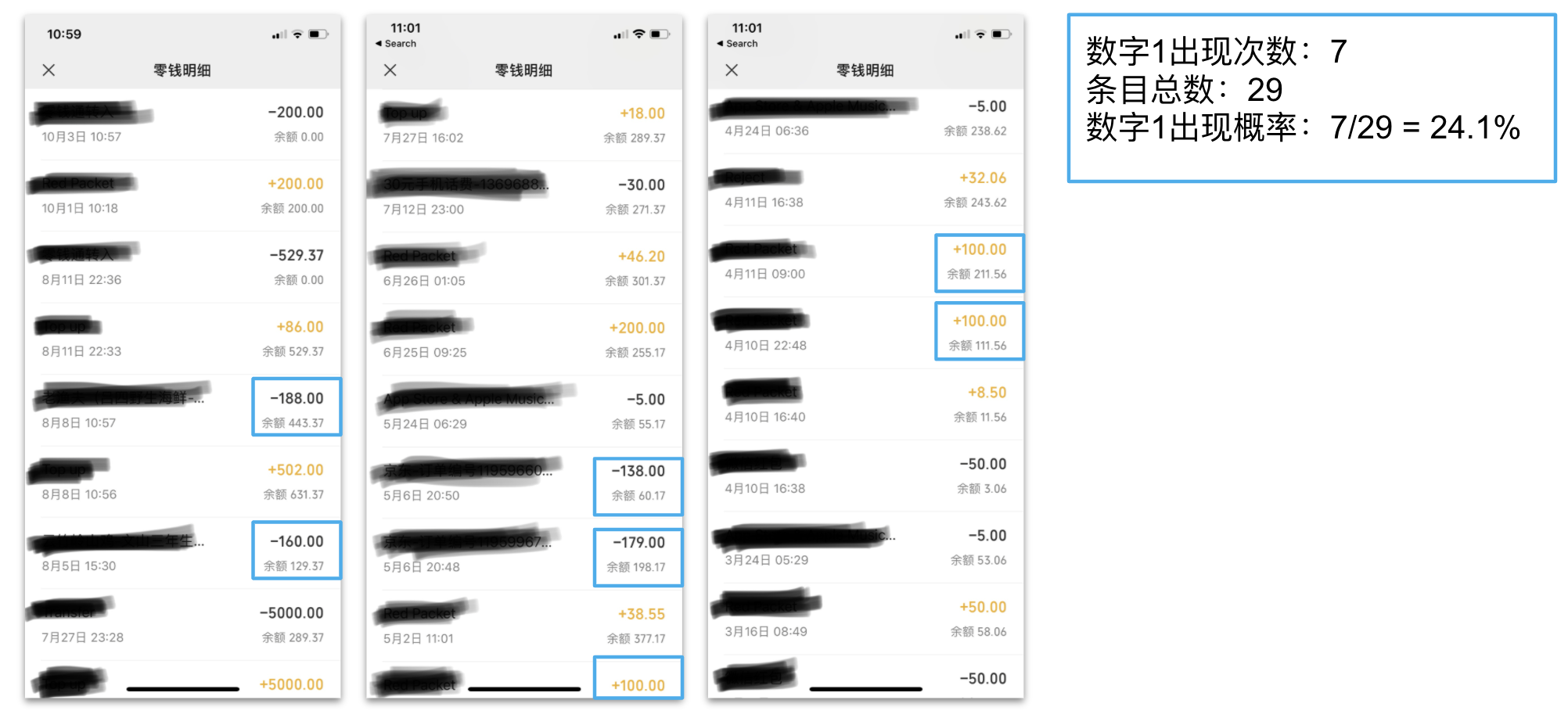
新冠日新增数据其实也在 Benford’s law 的适用范围内，那么如果数据真实的话，1打头的概率也应该远高于其他数字。我从 Our World in Data上下载了各国日新增的数据，然后统计了英国、美国、中国、伊朗的日新增首位数字的分布（感谢R包开发者Carlos Cinelli），结果如下：

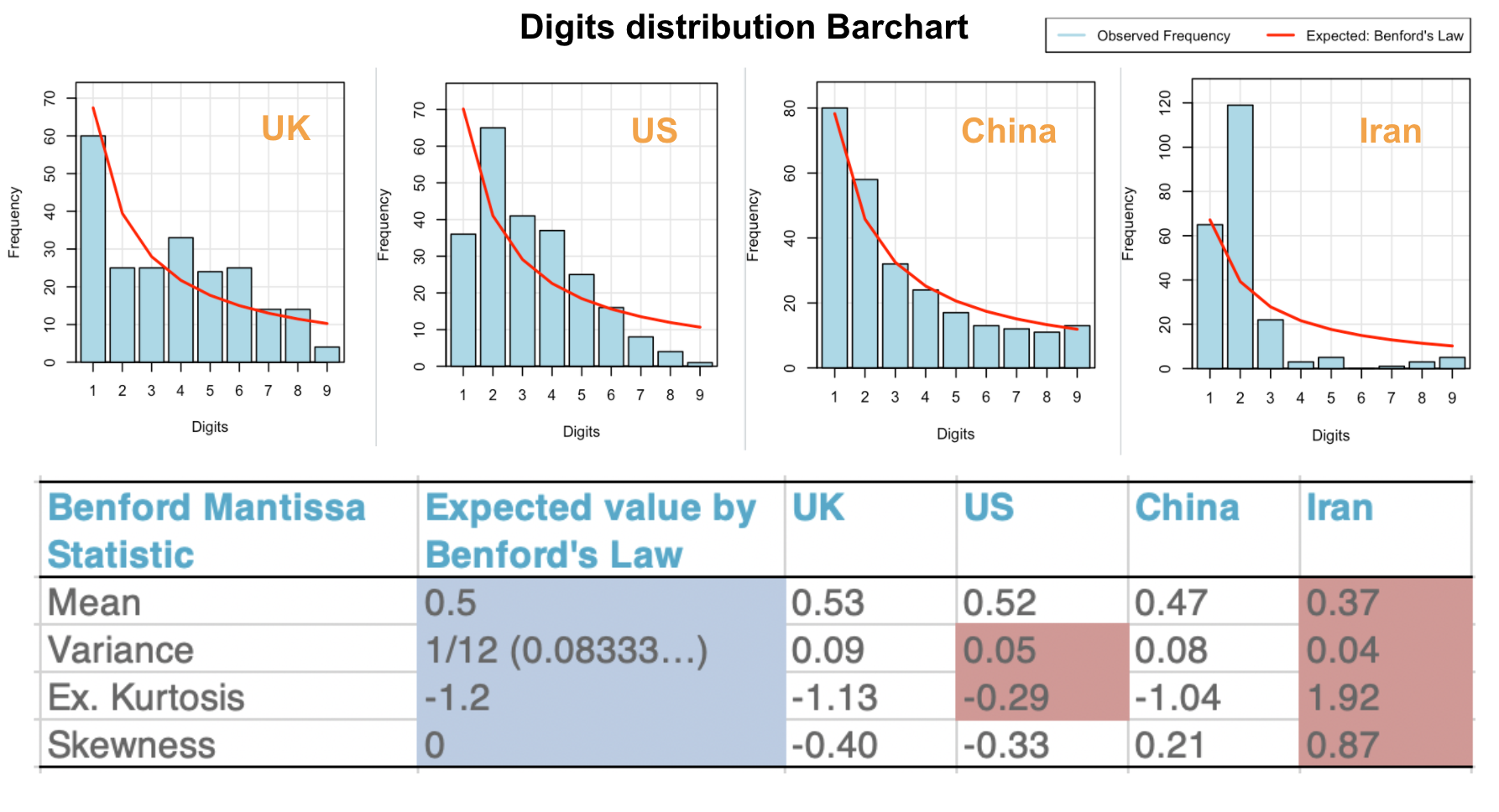
中国的数据居然出乎意料地符合定律，不仅分布图符合预期，统计结果也与预期十分相近，甩伊朗好几条街，符合程度甚至赶超英美。当然，这个定律早已被四大会计师事务所大规模应用（用来鉴别3000条目以上的数据），所以内行人想造假也不难。不过即便是造假，至少也说明中国的数据科学家敬业，在细节方面做到了一丝不苟。

关于 Benford’s law, 其实还有几个趣味八卦（感谢Andrie Jamain (2001)的论文)。这个定律虽然以物理学家 Benford 命名，但最早发现这个规律的人是 Newcomb。当时计算机计算器都没有发明出来，连顶级数学家，想算对数也只能查表。这个表00后可能见都没见过，不过印象中我用过的数学课本还是有这样的附录的。

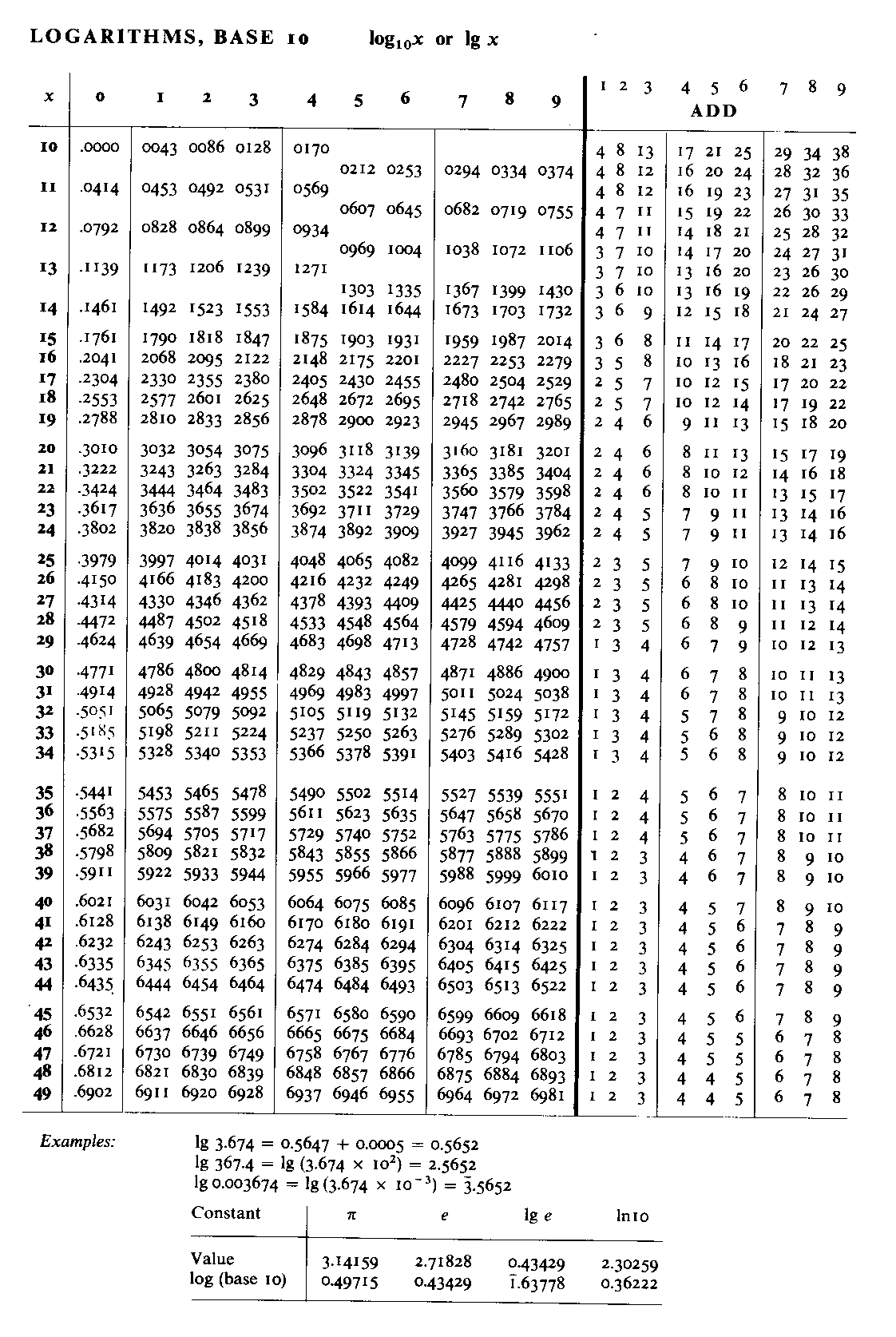
Newcomb就发现对数表前几页及前几行很快就被翻烂摸脏，后面却崭新得很,于是乎他就用两页纸记录了这个生活小观察, 并发表在 American Journal of Mathematics 上（1881年），他的原文如下：

That the ten digits do not occur with equal frequency must be evident to any one making much use of logarithmic tables, and noticing how much faster the first ones wear out than the last ones

论文中还简单列举了下1~9出现在首位及第二位的概率。

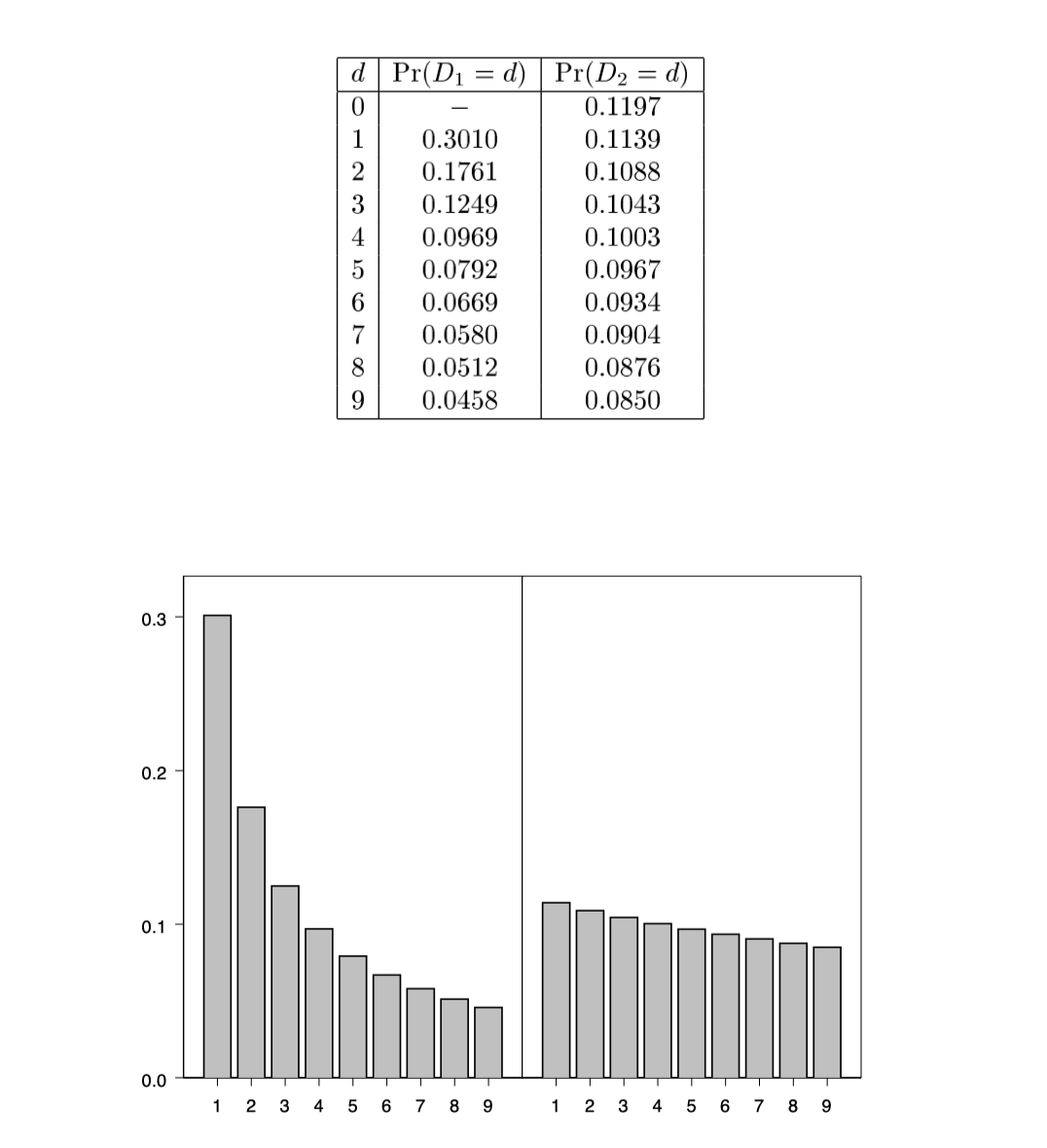
然后这个理论就被大伙儿遗忘了50年。直到Benford查对数表时发现1开头的数字都被指纹压花看不清了，才把这个定律重新发现了一次。当然 Benford也不光光是靠运气，他还是相当努力的。他不仅把这个定律用优美的数学符号写出来，还搜罗了各类数据，手动统计了数据，把这个定律检验得八九不离十。

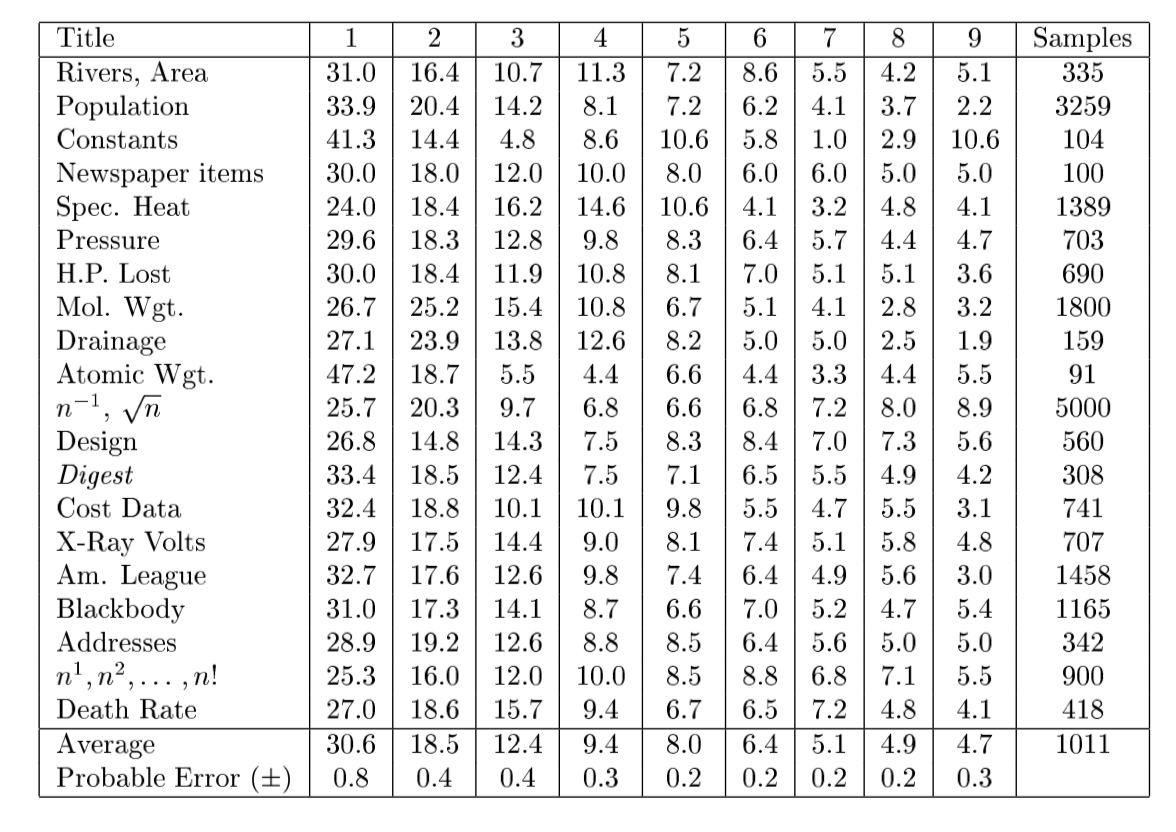
回顾完对数表，我还有个小发现，那就是对一个数取对数，得到的结果里首数叫characteristic，尾数叫mantissa（比如说Log11 = 1.04,首数是1，尾数是0.04）。显然，首数比尾数重要得多，于是characteristic也就有了特征这个引申义。

看来很多有趣的定律就躺在青天白日之下，以后我要继续挖掘！